封头展开
封头的展开较筒节复杂,有些封头,如椭圆形封头、球形封头和折边锥形封头,属于不可展开的零件,它们从坯料制成零件后,中性层尺寸发生变化。因此,这类零件的坯料计算比较复杂。
平封头
通常,平封头的毛坯尺寸有下列两种计算方法.
a.周长法
假定毛坯直径D0等于平封头纵截面的周长,并考虑一定的加工余量。
D0=d2+π(r+S/2)+2h+2δ
式中δ--封头边缘的机械加工余量,通常为15~40mm。
其余各符号见下图。
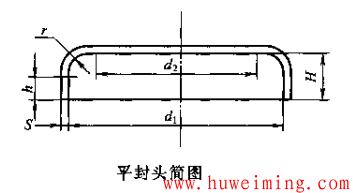
生产实践表明,按此式计算所得的平封头毛坯直径是偏大的,应根据实际生产情况予以适当修正。
下式是以周长法为基础的经验计算式:
D0=d1+r+1.5S+2h
当h>5%d1时,式中2h值应以(h+5%d1)代入。
b.面积法
假定封头毛坯面积等于成形封头的面积,再考虑一定的加工余量。为了简化计算公式,可以忽略不计圆角半径r。此时,计算公式为
πD02/4=π(d1+S)2/4+π(d1+S)(H+δ)
由此可得:
D0=SQRT((d1+S)2+4(d1+S)(H+δ))
椭圆形封头
椭圆形封头的形状较复杂,通常其毛坯直径都是用近似计算方法来确定的。下图为椭圆形封头简图。
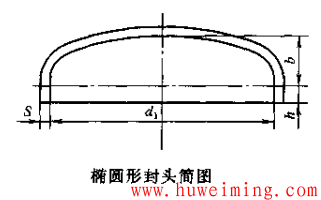
a.周长法
对于椭圆形封头来说,由于椭圆的半周长计算公式是比较复杂的。为了便于实际应用,必须加以适当简化。采用不同的简化方法,便会得到不同的计算公式。
椭圆半周长的近似计算公式:
P=πSQRT(2(a2+b2)-(a-b)2/4)/2
式中P--封头椭圆形部分的半周长,
a--椭圆的半长轴,
b--椭圆的半短轴。
封头毛坯直径D0在考虑了一定的加工余量后,可按下式计算,
D0=P+2hK0+2δ
式中K0--封头冲压成形时的拉伸系数,通常可取为0.75;
δ--封头边缘的机械加工余量,通常为15~40mm。
按此式计算椭圆形封头的毛坯直径比较繁复。对于a=2b(即d1=4b)的标准椭圆形封头,就可得到更简单的计算公式:
D0=1.223d1+2hK0+2δ
b.面积法
假定封头毛坯面积等于椭圆形封头中性层的面积。椭圆形封头中性层的面积应等于半椭圆球体面积与封头直边部分(包括必要的加工余量)面积之和,即:
F=Fe+Fs
半椭球体面积
Fe=πa2+πb2ln((1+K)/(1-K))/(2K)
式中a--椭球体中性层的半长轴,
a=(d1+S)/2
b--椭球体中性层的半短轴,
K--椭圆率,
K=SQRT(a2-b2)/a
令m=a/b,得:
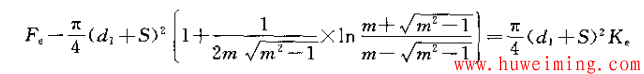
其中

考虑了加工余量的封头直边部分面积
Fs=π(d1+S)(h+δ)
封头毛坯面积:
F0=πD0/4
且
F0=F=Fe+Fs
最后可得封头毛坯直径
D0=SQRT((d1+S)2Ke+4(d1+S)(h+δ))
对于标准椭圆形封头(d1=4b),可算得Ke=1.38。此时:
D0=SQRT(1.38(d1+S)2+4(d1+S)(h+δ))
除了上述两种计算公式之外,还有许多经验计算方法,如:D0=1.2(d1+S)+2h等,均可在一定范围内应用。
球形封头
球形封头的毛坯尺寸通常根据面积法计算。此时:
πD02/4=πd2/2+πd(h+δ)
D0=SQRT(2d2+4d(h+δ))
式中δ--球形封头边缘的机械加工余量,通常为15~40mm。
其余符号见下图。
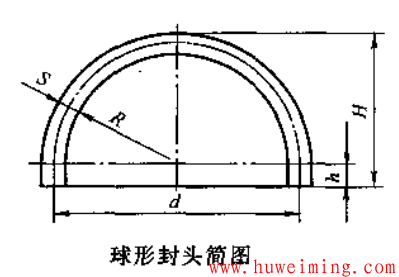
此外,也可按近似公式计算:
D0=1.43d+2h
由于封头成形过程中受模具间隙、加热温度、压边力大小等到具体工艺条件的影响,封头坯料尺寸可作适当修正。目前,很多企业会根据自己的经验整理出一些既简单又实用的坯料计算经验公式。
注:SQRT为开平方根。


